HERS Rater Math Problems For People That Hate Math
FREE HERS RATER PRACTICE EXAMALREADY A HERS ENERGY AUDITOR?Get the only Energy Auditor Marketing Newsletter with monthly strategies and tactics to grow your home performance business.
|
You are not alone, math is typically the most disliked topic on the HERS Rater Exam. It can be confusing when to use the right equation or the difference between the ACH and MRV equations. This section will help walk you through the math equations on the HERS Rater exam.
You will see 11 different types of equations and math problems on the HERS Rater exam. None of them are more than 4 steps so don't get overwhelmed. With practice and repetition these math questions become easier and easier to do. 1. Conversions - kWh, watts, therms, & BTU'sCommon questions on the HERS Rater exam and HERS Rater practice exams ask you to convert between units of power and energy (multiply power by time) or between kWh, therms and BTU's. Some important conversions that you will just have to remember are:
If you are given BTU and need to find kWh, therms or CCF (or any other energy unit)...
DIVIDE BTU'S BY YOUR MAGIC CONVERSION NUMBER If you are given kWh, therms or CCF and need to convert to BTU's... MULTIPLY kWh, THERMS ETC BY YOUR MAGIC CONVERSION NUMBER A BTU is the universal language of energy. It doesn't matter if you have gas or electric appliances, therms, CCF or kWh in your bill, it all can be converted to BTUs to find and compare things like:
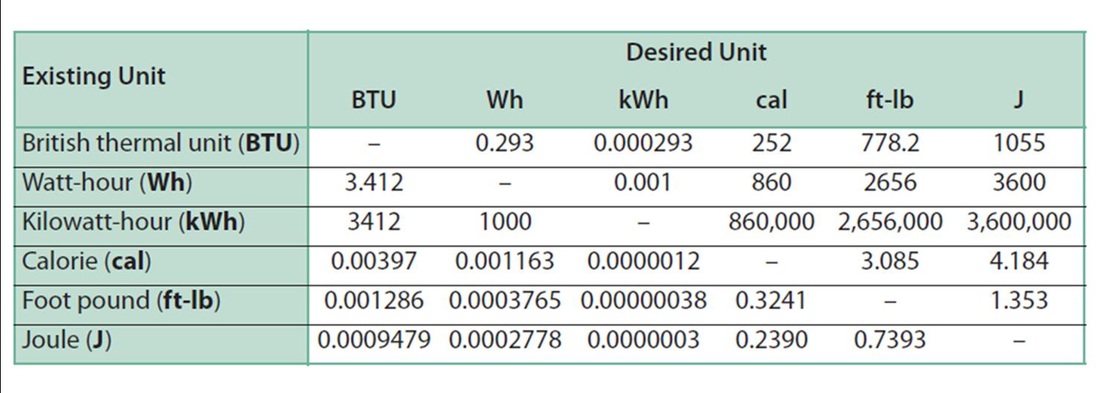
You can also use the conversion table below to switch between units of energy (power is a different table). To use the table, start with what unit you are given and find it and go down in the "Existing Unit" column. Then go across horizontally to the "Desired Unit" to the right and find the unit you need to convert it to. The number you reach is your magic conversion number you can use by just multiplying your given "Existing Unit" number by the magic conversion number just found to get units of your "Desired Unit." Here is a BPI sample question on conversions. 1. Find the amount of energy used in BTU's of a 60 watt light bulb which is on for 2 hours. Answer: Given 60 watts (units of power, we want energy) and its running for 2 hrs. We will use the formula: Energy = Power x time Energy = 60 watts x 2 hrs Energy = 120 watt-hrs Now let convert watt-hrs to BTUs. If you first try to convert watts to BTU using the table, you will find there is no unit for just watts in the table! That should tell you that you need to convert it first. Now we can find watt-hrs our table and go across until you hit the BTU column. What is the magic conversion number? It is 3.412. So we just multiply our given energy use (120 watt-hrs) by the magic conversion factor for the answer. 120 watt-hrs x 3.412 = 409.44 BTU
Now to get comfortable with this, let's find how many watt-hrs is in 409.44 BTU using our table. 409.44 BTU x (magic conversion number) = watt-hrs 409.44 BTU x 0.293 = 119.966 or rounding up we get 120 watt-hrs, the same answer we started with! 2. Cost and Energy UseCost Calculations
Finding the cost to operate a furnace or appliance should always be last, after you have found the energy use. You will be given to utility rate ($0.11 a kWh or $1.20 per therm) and you have to find the energy use. Energy Use Calculations You will be given the power use (BTU/hr or kW) and a time the appliance is running, (5 hrs for 10 days). You just need to multiple the one by the other. You may have to do some conversions here to therms, kWh or CCF to BTUs (our universal language). See the section above about multiplying or dividing by our magic conversion number. Here is a BPI sample question on cost and energy use. 2. Find the electrical use of a furnace using 800 watts of power running 5 hours a day for 12 days. Answer: Given: time running = 5 hrs per day x 12 days = 60 hrs per day energy use = power x time = 800 watts x time = 800 watts x 60 hrs per day = 48,000 watts per hr per day or 48,000 watt-hrs 3. Using information from problem 2 above, how much does it cost to run the furnace if the electrical rate is $0.20 per kWh? Answer: energy use = 48,000 watt-hrs, we need to convert watts to kWh by multiplying by 0.001 or dividing by 1000, whatever you prefer. watt-hrs converted to kWh 48,000 watt-hrs x 0.001 kWh/watt-hrs = 48 kWh or 48,000 watt-hrs / 1,000 watt-hrs/kWh = 48 kWh 48 kWh x utility rate = cost 48 kWh x $0.20 per kWh = $9.6 per kWh 3. Payback and SIRPayback = cost / savings
SIR = savings x life / cost Any SIR greater than 1 is good A good rule of thumb to ask yourself, "does this make sense?" If your appliance cost $2,000 and your annual savings is only $300, does it make sense that your payback is less than a year (0.15 if you took the formula flipped)? If not, try flipping your equations around and don't pick the answer on the exam too fast. 4. Windows and Arealength x width = area
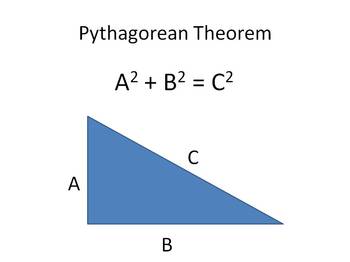
If you are given a wall, door and window find the total area of the wall, then subtract the area of the window and door out of the total to find the net wall area. Find a missing side or roof length given the base and height - use Pythagorean Theorem Let's do a sample problem you might see on the BPI exam with area and the Pythagorean theorem.
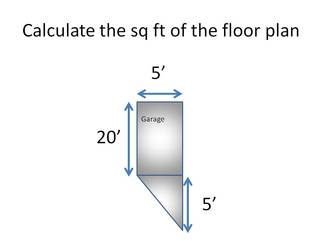
Let's tackle this by breaking up the garage floor plan into two parts and finding the area for each section
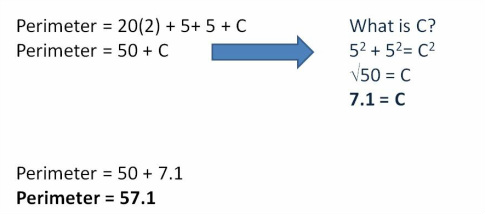
Garage 1: 20’ x 5’ = 100 sq ft Garage 2: treat the triangle as a 5’ x 5’ box; area of box is 25 sq ft; 25 sq ft / 2 = 12.5 sq ft Garage 1 + Garage 2 = total sq ft 100 + 12.5 = 112.5 sq ft Now, let's find the perimeter of the garage floor plan above. Garage 2 option 2: use the Pythagorean theorem to find the length of the missing side and then add the outer lengths together. 5. R-value and U-value1/R = U-value
1/U = R-value U-values are for the total composite of an object such as a window (sash, frame, air space, glass, low-e coating) or entire wall (including frame, felt paper, insulation, drywall). U-values can not be added, but can be multiplied. R-values are for just one component and can be added together. Given the U-value, you find the R-value by by taking 1 over the U-value. Given the R-value, you can find the U-value by taking 1 over the R-value. 6. HDD and CDD - Heating Degree Day and Cooling Degree DayBalance point of HDD = 65 degrees
Balance point of CDD = 78 degrees The HDD is a tool for predicting heating costs.
Example: Today's temperature was 10 degrees as a low and 40 degrees as a high. What is the HDD?
7. MVR - Minimum Ventilation RequirementMVR = 0.35 x Volume / 60
8. ACHCFM50 x 60 / Volume
9. Baseline and Seasonal Useage
10. DraftNext Section |